はじめに
離散時間信号をアンダー・サンプリングした結果のDTFTと元の離散時間信号のDTFTの関係を明らかにし、エイリアシングが生じない条件を導く。
本記事の内容は下記の資料にも記した。
Release v0.11.1 · motchy869/Signal-Processing-Memorandum (github.com)
「アンダー・サンプリングされた信号のDTFT」
\[
% general purpose
\newcommand{\ctext}[1]{\raise0.2ex\hbox{\textcircled{\scriptsize{#1}}}}
% mathematics
% general purpose
\DeclarePairedDelimiterX{\parens}[1]{\lparen}{\rparen}{#1}
\DeclarePairedDelimiterX{\braces}[1]{\lbrace}{\rbrace}{#1}
\DeclarePairedDelimiterX{\bracks}[1]{\lbrack}{\rbrack}{#1}
\DeclarePairedDelimiterX{\verts}[1]{|}{|}{#1}
\DeclarePairedDelimiterX{\Verts}[1]{\|}{\|}{#1}
\newcommand{\as}{{\quad\textrm{as}\quad}}
\newcommand{\st}{{\textrm{ s.t. }}}
\DeclarePairedDelimiterX{\setComprehension}[2]{\lbrace}{\rbrace}{#1\,\delimsize\vert\,#2}
\newcommand{\naturalNumbers}{\mathbb{N}}
\newcommand{\integers}{\mathbb{Z}}
\newcommand{\rationalNumbers}{\mathbb{Q}}
\newcommand{\realNumbers}{\mathbb{R}}
\newcommand{\complexNumbers}{\mathbb{C}}
\newcommand{\field}{\mathbb{F}}
\newcommand{\func}[2]{{#1}\parens*{#2}}
\newcommand*{\argmax}{\operatorname*{arg~max}}
\newcommand*{\argmin}{\operatorname*{arg~min}}
% set theory
\newcommand{\range}[2]{\braces*{#1,\dotsc,#2}}
\providecommand{\complement}{}\renewcommand{\complement}{\mathrm{c}}
\newcommand{\ind}[2]{\mathbbm{1}_{#1}\parens*{#2}}
\newcommand{\indII}[1]{\mathbbm{1}\braces*{#1}}
% number theory
\newcommand{\abs}[1]{\verts*{#1}}
\newcommand{\combi}[2]{{_{#1}\mathrm{C}_{#2}}}
\newcommand{\perm}[2]{{_{#1}\mathrm{P}_{#2}}}
\newcommand{\GaloisField}[1]{\mathrm{GF}\parens*{#1}}
% real analysis
\newcommand{\NapierE}{\mathrm{e}}
\newcommand{\sgn}[1]{\operatorname{sgn}\parens*{#1}}
\newcommand*{\rect}{\operatorname{rect}}
\newcommand{\cl}[1]{\operatorname{cl}#1}
\newcommand{\Img}[1]{\operatorname{Img}\parens*{#1}}
\newcommand{\dom}[1]{\operatorname{dom}\parens*{#1}}
\newcommand{\norm}[1]{\Verts*{#1}}
\newcommand{\floor}[1]{\left\lfloor#1\right\rfloor}
\newcommand{\ceil}[1]{\left\lceil#1\right\rceil}
\newcommand{\expo}[1]{\exp\parens*{#1}}
\newcommand{\sinc}{\operatorname{sinc}}
\newcommand{\nsinc}{\operatorname{nsinc}}
\newcommand{\GammaFunc}[1]{\Gamma\parens*{#1}}
\newcommand*{\erf}{\operatorname{erf}}
% inverse trigonometric functions
\newcommand{\asin}[1]{\operatorname{Sin}^{-1}{#1}}
\newcommand{\acos}[1]{\operatorname{Cos}^{-1}{#1}}
\newcommand{\atan}[1]{\operatorname{{Tan}^{-1}}{#1}}
\newcommand{\atanEx}[2]{\atan{\parens*{#1,#2}}}
% convolution
\newcommand{\cycConv}[2]{{#1}\underset{\text{cyc}}{*}{#2}}
% derivative
\newcommand{\deriv}[3]{\frac{\operatorname{d}^{#3}#1}{\operatorname{d}{#2}^{#3}}}
\newcommand{\derivLong}[3]{\frac{\operatorname{d}^{#3}}{\operatorname{d}{#2}^{#3}}#1}
\newcommand{\partDeriv}[3]{\frac{\operatorname{\partial}^{#3}#1}{\operatorname{\partial}{#2}^{#3}}}
\newcommand{\partDerivLong}[3]{\frac{\operatorname{\partial}^{#3}}{\operatorname{\partial}{#2}^{#3}}#1}
\newcommand{\partDerivIIHetero}[3]{\frac{\operatorname{\partial}^2#1}{\partial#2\operatorname{\partial}#3}}
\newcommand{\partDerivIIHeteroLong}[3]{{\frac{\operatorname{\partial}^2}{\partial#2\operatorname{\partial}#3}#1}}
% integral
\newcommand{\integrate}[5]{\int_{#1}^{#2}{#3}{\mathrm{d}^{#4}}#5}
\newcommand{\LebInteg}[4]{\int_{#1} {#2} {#3}\parens*{\mathrm{d}#4}}
% complex analysis
\newcommand{\conj}[1]{\overline{#1}}
\providecommand{\Re}{}\renewcommand{\Re}[1]{{\operatorname{Re}{\parens*{#1}}}}
\providecommand{\Im}{}\renewcommand{\Im}[1]{{\operatorname{Im}{\parens*{#1}}}}
\newcommand{\Arg}{\operatorname{Arg}}
\newcommand{\Log}{\operatorname{Log}}
% Laplace transform
\newcommand{\LPLC}[1]{\operatorname{\mathcal{L}}\parens*{#1}}
\newcommand{\ILPLC}[1]{\operatorname{\mathcal{L}}^{-1}\parens*{#1}}
% Discrete Fourier Transform
\newcommand{\DFT}[1]{\mathrm{DFT}\parens*{#1}}
% Z transform
\newcommand{\ZTrans}[1]{\operatorname{\mathcal{Z}}\parens*{#1}}
\newcommand{\IZTrans}[1]{\operatorname{\mathcal{Z}}^{-1}\parens*{#1}}
% linear algebra
\newcommand{\bm}[1]{{\boldsymbol{#1}}}
\newcommand{\matEntry}[3]{#1\bracks*{#2}\bracks*{#3}}
\newcommand{\matPart}[5]{\matEntry{#1}{#2:#3}{#4:#5}}
\newcommand{\diag}[1]{\operatorname{diag}\parens*{#1}}
\newcommand{\tr}[1]{\operatorname{tr}{\parens*{#1}}}
\newcommand{\inprod}[2]{\left\langle#1,#2\right\rangle}
\newcommand{\HadamardProd}{\odot}
\newcommand{\HadamardDiv}{\oslash}
\newcommand{\Span}[1]{\operatorname{span}\bracks*{#1}}
\newcommand{\Ker}[1]{\operatorname{Ker}\parens*{#1}}
\newcommand{\rank}[1]{\operatorname{rank}\parens*{#1}}
% vector
% unit vector
\newcommand{\vix}{\bm{i}_x}
\newcommand{\viy}{\bm{i}_y}
\newcommand{\viz}{\bm{i}_z}
% graph theory
\newcommand{\neighborhood}{\mathcal{N}}
% probability theory
\newcommand{\PDF}[2]{\operatorname{PDF}\bracks*{#1,\;#2}}
\newcommand{\Ber}[1]{\operatorname{Ber}\parens*{#1}}
\newcommand{\Beta}[2]{\operatorname{Beta}\parens*{#1,#2}}
\newcommand{\ExpDist}[1]{\operatorname{ExpDist}\parens*{#1}}
\newcommand{\ErlangDist}[2]{\operatorname{ErlangDist}\parens*{#1,#2}}
\newcommand{\PoissonDist}[1]{\operatorname{PoissonDist}\parens*{#1}}
\newcommand{\GammaDist}[2]{\operatorname{Gamma}\parens*{#1,#2}}
\newcommand{\cind}[2]{\ind{#1\left| #2\right.}} % conditional indicator function
\providecommand{\Pr}{}\renewcommand{\Pr}[1]{\operatorname{Pr}\parens*{#1}}
\DeclarePairedDelimiterX{\cPrParens}[2]{(}{)}{#1\,\delimsize\vert\,#2}
\newcommand{\cPr}[2]{\operatorname{Pr}\cPrParens{#1}{#2}}
\newcommand{\E}[2]{\operatorname{E}_{#1}\bracks*{#2}}
\newcommand{\cE}[3]{\E{#1}{\left.#2\right|#3}}
\newcommand{\Var}[2]{\operatorname{Var}_{#1}\bracks*{#2}}
\newcommand{\Cov}[2]{\operatorname{Cov}\bracks*{#1,#2}}
\newcommand{\CovMat}[1]{\operatorname{Cov}\bracks*{#1}}
% signal processing
% Discrete Time Fourier Transform
\newcommand{\DTFT}[1]{\mathrm{DTFT}\parens*{#1}}
\newcommand{\IDTFT}[1]{\mathrm{IDTFT}\parens*{#1}}
% computer science
% programming
\newcommand{\plpl}{\mathrel{++}}
\newcommand{\pleq}{\mathrel{+}=}
\newcommand{\asteq}{\mathrel{*}=}
\]
\[
\newcommand{\Ts}{T_\text{s}}
\newcommand{\xd}{x_\text{d}}
\newcommand{\yd}{y_\text{d}}
\newcommand{\Xd}{X_\text{d}}
\newcommand{\Yd}{Y_\text{d}}
\newcommand{\DTFT}[1]{\mathrm{DTFT}\parens*{#1}}
\newcommand{\DTFTwithArg}[2]{\DTFT{#1}\parens*{#2}}
\newcommand{\IDTFT}[1]{\mathrm{IDTFT}\parens*{#1}}
\newcommand{\IDTFTwithArg}[2]{\IDTFT{#1}\parens*{#2}}
\]
主張
記号を次のように定義する。
- $R\in\naturalNumbers,\;R\geq 2$ : アンダー・サンプリング・レート
- $\xd:\integers\to\complexNumbers$ : 離散時間信号
- $\Ts>0$ : $\xd$ のサンプル周期
- $\yd$ : $\xd$ を $1/R$ にアンダー・サンプリングした離散時間信号。つまり $\yd(n) = \xd(nR)$ 。
- $\Xd$ : $\xd$ のDTFT
- $\Yd$ : $\yd$ のDTFT
このとき $Y$ は次式で表される。
\[ \Yd(\omega) = \frac{1}{R}\sum_{n=0}^{R-1} \Xd\parens*{\omega-n\frac{2\pi}{R\Ts}} \]
$\Yd$ は $\omega$ に関する $2\pi/(R\Ts)$ 周期関数となり、$\Yd$ の第1 Nyquist 領域は $S_{\text{N},Y} \coloneqq [-\pi/(R\Ts),-\pi/(R\Ts))$ となる。
全体に $1/R$ が掛けられているが、振幅が $1/R$ になるわけではない。DTFT の内積計算の対象となる点の数が $1/R$ に減ったことに起因する。
$\Xd$ の台のうち $\xd$ の第1 Nyquist 領域 $S_{\text{N},X} \coloneq [-\pi/\Ts, \pi/\Ts)$ にある部分を $S_X$ とする。エイリアシングが生じない必要十分条件は $S_X\subset S_{\text{N},X}$ である。ここで言うエイリアシングとは、$S_X$ を $2\pi/(R\Ts)$ の整数倍ずつ平行移動しながら無限に複製したものを考えたとき、複製された $S_X$ 同士に重なりが生じることを指す。
導出
\[
\begin{align*}
\Yd(\omega) &= \sum_{n=-\infty}^\infty \yd(n)\exp(-i\omega nR\Ts) = \sum_{n=-\infty}^\infty \xd(nR)\exp(-i\omega nR\Ts) \\
&= \sum_{m=-\infty}^\infty u(m)\xd(m)\exp(-i\omega m\Ts) \quad \text{where} \quad u(m) \coloneqq \begin{cases}
1 & (m\in R\integers) \\
0 & (\text{otherwise})
\end{cases} \\
&= \DTFTwithArg{u\xd}{\omega} \\
&= \frac{\Ts}{2\pi}\integrate{-\pi/\Ts}{\pi/\Ts}{\Xd(\omega-\tilde{\omega})U(\tilde{\omega})}{}{\tilde{\omega}} \quad \text{where} \quad U(\omega) \coloneqq \frac{2\pi}{R\Ts}\sum_{m=-\infty}^\infty\delta\parens*{\omega – n\frac{2\pi}{R\Ts}} \\
&= \frac{1}{R} \integrate{-\pi/\Ts}{\pi/\Ts}{\Xd(\omega-\tilde{\omega})\sum_{n=-\infty}^{\infty}\delta\parens*{\tilde{\omega}-n\frac{2\pi}{R\Ts}}}{}{\tilde{\omega}} \tag{1}
\end{align*}
\]
※1 信号処理 Tips – 門前の小僧 (motchy869.com)「指数関数とデルタ関数の無限級数」を用いた
被積分関数の $\Xd$ とデルタ関数列を次の図に示す。$\omega$ がデルタ関数列の原点からのオフセットである。
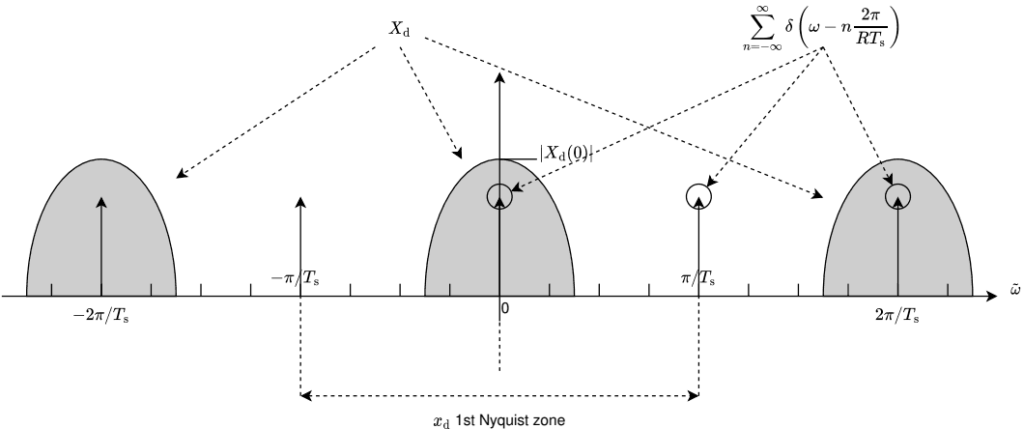 $\Xd$ とデルタ関数列($R=2$)
$\Xd$ とデルタ関数列($R=2$)
$\Xd$ が $2\pi/\Ts$ 周期関数であること、式(1)の積分範囲が $[-\pi/\Ts,\pi/\Ts]$ であること、および $R$ が偶数の場合に積分範囲の両端点で生じる、デルタ関数の中心から左右半分と $\Xd$ との積の積分を考慮すると、式(1)は次式と等しいことが解る。
\[
\begin{align*}
\Yd(\omega) &= \frac{1}{R}\sum_{n=-\floor{R/2}}^{\floor{R/2}} \integrate{-\pi/\Ts}{\pi/\Ts}{\Xd(\omega-\tilde{\omega})\delta\parens*{\tilde{\omega}-n\frac{2\pi}{R\Ts}}}{}{\tilde{\omega}} \\
&= \frac{1}{R}\sum_{n=0}^{R-1} \Xd\parens*{\omega-n\frac{2\pi}{R\Ts}}
\end{align*}
\]
また同時に、$\Yd$ が $\omega$ に関する $2\pi/(R\Ts)$ 周期関数であることも解る。
エイリアシングが生じないことと $S_X \subset S_{N,\text{X}}$ が同値であることが解る。$\Yd$ を次の図に示す。
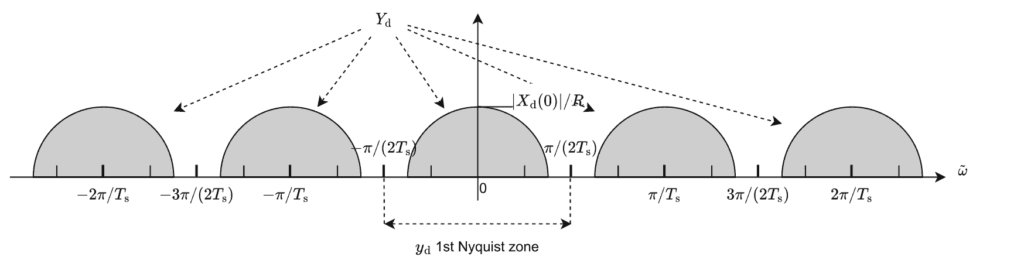 $\Yd$
$\Yd$
数値例
$x(t) = A\exp(-t^2/(2\sigma^2))$ とし、特に $A=1,\;\sigma=1/10,\;\Ts=1/80,\;R=2$ としたときの数値例を示す。$\xd$ は $[-5\sigma,5\sigma]$ からサンプリングし、ポイント数は $2\times 5\sigma/\Ts + 1 = 81$ である。
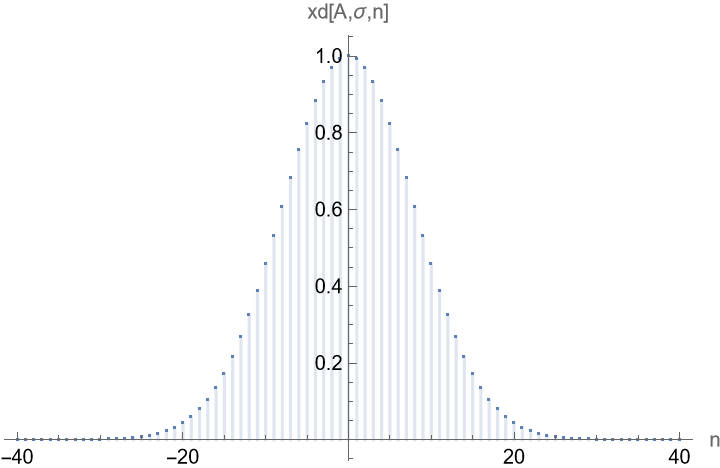 $\xd$
$\xd$
これを $1/R=1/2$ にアンダー・サンプリングして $\yd$ を得る(下図)。
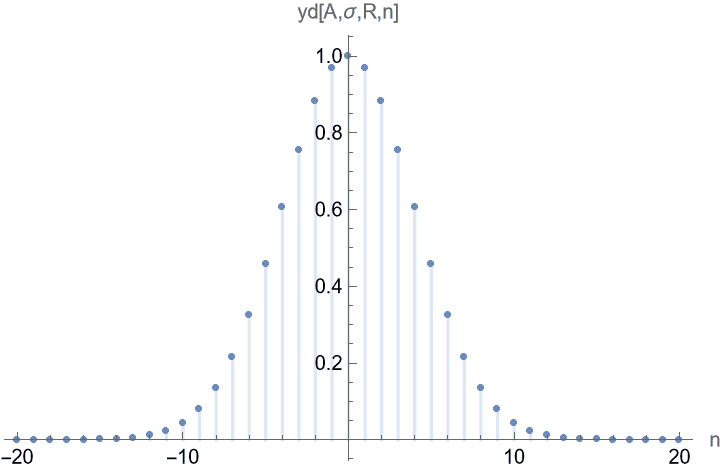 $\yd$
$\yd$
$\xd,\yd$ それぞれの DTFT $\Xd,\Yd$ を計算する(下図)。
![2023_4_23_1352_Abs[Xd].png](https://motchy869.com/wordpress/wp-content/uploads/2023/04/2023_4_23_1352_AbsXd.png) $\abs{\Xd}$
$\abs{\Xd}$
![2023_4_23_1352_Abs[Yd].png](https://motchy869.com/wordpress/wp-content/uploads/2023/04/2023_4_23_1352_AbsYd.png) $\abs{\Yd}$
$\abs{\Yd}$
$\Yd$ の最大値が $\Xd$ の最大値の半分であり、 $\yd$ の第1 Nyquist 領域が $\xd$ の半分に狭まっていることを確認できる。




![2023_4_23_1352_Abs[Xd].png](https://motchy869.com/wordpress/wp-content/uploads/2023/04/2023_4_23_1352_AbsXd.png)
![2023_4_23_1352_Abs[Yd].png](https://motchy869.com/wordpress/wp-content/uploads/2023/04/2023_4_23_1352_AbsYd.png)