目次
経緯
物理以外の参考書等(例えば制御工学)で拘束条件付きの問題に対して最初から一般化座標系を導入して拘束条件なしのLagrangeの運動方程式を立てている様子を見て、それが直角座標系に於けるNewtonの運動方程式と等価であることを納得したくて暫く考えていた。その結果をここに書き残しておく。
はじめに
まず直角座標系に於いて拘束条件付きのLagrangeの運動方程式がNewtonの運動方程式と同値であることを理解する。そして、可逆な座標変換、所謂「一般化座標系」への変換を行ってもLagrangeの運動方程式が表面的には形を変えない(Lagrange関数$L$の数式は変わるが、それを相変わらず$L$と書く限り形を変えない)ことを示す。そして拘束条件を表す制約式に現れる一般化座標変数の個数が最小となるような変換を選ぶと、一般化座標変数の一部が拘束条件から容易に求まることと、残りの一般化座標変数について拘束条件が消える可能性について述べる。最後に、そのことを確認できる例題を一つ紹介し、数値計算結果を示す。
問題設定
$N$を質点の個数とし、$m_i\;(i=1,\dotsc,N)$を$i$番目の質点(以下「質点$i$」と呼ぶ)の質量とする。各質点に働く力は保存力、および質点の速度と直角に働く(つまり質点に対して仕事をしない)拘束力のみであるとする。ここでの拘束力とは、質点がある曲面や曲線に沿ってしか運動できず、かつそれら曲面,曲線を構成する物体(拘束物)と質点の間に摩擦力が生じない状況で、質点が拘束物から受ける力を想定する(例えば滑らかなワイヤに通されたビーズの運動や、半径が異なる、中心を共有する2つの滑らかな球面の間に挟まった鉄球の運動などを想像するとよい)。
直角座標系では質点1個あたり3つの座標変数があるので、系全体では$3N$個の座標変数がある。これらを$\bm{r} = [r_1,r_2,\dotsc,r_{3N}]^\top \in \realNumbers^{3N}$とする。質点$i$の座標は$[r_{3i-2}, r_{3i-1}, r_{3i}]^\top$となる。個々の質点の座標を分けて考えるのではなく$\bm{r}$にまとめて表現することで、質点系を$3N$次元空間を運動する1個の高次元の質点として扱える。このようにしても数学的には元の運動方程式と変わらない。
保存力
直角座標系に於いて、質点系に保存力をもたらすポテンシャルを$\VC:\bm{r} \in \realNumbers^{3N} \mapsto \VC(\bm{r}) \in \realNumbers$とする(CはCartesianのC)(空間に固く固定された電荷などポテンシャルの原因が複数あるときはそれらの和を$\VC$とすればよい)。質点系が受ける保存力は$-\nabla_\bm{r}\VC(\bm{r})$となる。
Lagrange関数
直角座標系に於けるLagrange関数を$\LC: (t,\bm{r},\dot{\bm{r}}) \in \realNumbers\times\realNumbers^{3N}\times\realNumbers^{3N} \mapsto \LC(t,\bm{r},\dot{\bm{r}}) \in \realNumbers$とすると
\[ \LC(t,\bm{r},\dot{\bm{r}}) = \sum_{i=1}^N \frac{1}{2}m_i\norm{\derivLong{[r_{3i-2}, r_{3i-1}, r_{3i}]}{t}{}}_2^2 – \VC(\bm{r}) = \frac{1}{2}\dot{\bm{r}}^\top M_\text{C}\dot{\bm{r}} – \VC(\bm{r}) \]ここに$M_\text{C}$は「質量行列」と呼ばれる対角行列であり、$M_{3i-2,3i-2} = M_{3i-1,3i-1} = M_{3i,3i} = m_i$である(直角座標系では対角であるが、他の座標系ではそうとも限らない)。
拘束条件
質点系の拘束条件は複数あり得る。$\NC$をその個数とする(CはConstraintのC)。これらの制約が、直角座標系において$\mathrm{C}^1$級の関数$\gCi:\bm{r} \in \realNumbers^{3N} \mapsto \gCi(\bm{r}) \in \realNumbers\;(i=1,\dotsc,\NC)$を用いて$\gCi(\bm{r}) = 0$と表される場合を考える($g$の添え字のCはCartesianのC)。但し各制約式$\gCi(\bm{r}) = 0$は、それが満足される領域で$\nabla \gCi \neq \bm{0}$となるように選ぶものとする(後で判るが、勾配が消えると計算上都合が悪い)。例えば質点1に対する制約条件として直線への拘束${r_1}^2 + {r_2}^2 = 0$を考えると、制約条件を満たす領域$r_1=r_2=0$で左辺の勾配$[2r_1,2r_2,0]^\top$が$\bm{0}$になる。しかし同じ拘束条件を、平面を表す2つの制約式$r_1=0,r_2=0$の連立として表現すれば勾配はそれぞれ$[1,0,0]^\top,\;[0,1,0]^\top \neq \bm{0}$となる。同様に曲線も曲面の交線として表現する。今回は不等式制約(物理的には壁に進入しない等に相当する)は扱わない。冒頭で仮定したように、質点が曲面から受ける拘束力は曲面に垂直、すなわち$\nabla \gCi$に平行である。
直角座標系に於けるLagrangeの運動方程式
以上に述べたことから、直角座標系に於ける拘束条件付きのNewtonの運動方程式は次のようになり、これは拘束条件付きのLagrangeの運動方程式(Lagrange’s equations of the first kind (第一種Lagrange方程式)とも呼ばれる)と同値である。
$$ \begin{align} \nabla_{\bm{r}}\LC(t,\bm{r},\dot{\bm{r}}) – \derivLong{\nabla_{\dot{\bm{r}}}\LC(t,\bm{r},\dot{\bm{r}})}{t}{} + \sum_{i=1}^{\NC} \lambda_i(t) \nabla_\bm{r} \gCi(\bm{r}) = \bm{0} \label{直角座標系に於けるNewtonの運動方程式} \\ \gCi(\bm{r}) = 0\;(i=1,\dotsc,N_C) \label{直角座標系に於ける制約条件式} \end{align} $$ここに$\lambda_i$は質点系の位置と加速度, 質点系に働く保存力に依存する、究極的には$t$の関数である。質点が拘束条件のレールからはみ出ないように$\nabla \gCi$に平行な力が働いて、質点系に働く慣性抗力(加速度と質量の積の-1倍)と質点系に働く保存力をキャンセルしていることは確かだが、いつどんな大きさで働くのかは自明ではない。そのため$\lambda_i$は$\bm{r}$と同時に解かねばならない。
可逆な座標変換をしてもLagrangeの運動方程式の形が変わらないこと
産業応用上解く必要に迫られる力学の問題は解析的に解けないものが殆どであり、数値解析に頼ることになるのだが、その場合でも前出の式\eqref{直角座標系に於けるNewtonの運動方程式},\eqref{直角座標系に於ける制約条件式}をできるだけ解きやすくなるように座標変換することは必要である。拘束条件を利用して解くべき座標変数の個数を減らせれば問題の次元が下がって扱いやすくなる。
$\bm{r} \in \realNumbers^{3N}$と$\bm{q} \in \realNumbers^{3N}$の間の可逆な$\mathrm{C}^2$級の座標変換を考える。つまり$\bm{r}$は$\bm{q}$の$\mathrm{C}^2$級関数$\bm{r}: \bm{q} \in \realNumbers^{3N} \mapsto \bm{r}(\bm{q}) \in \realNumbers^{3N}$として表せて、かつ$\bm{q}$も$\mathrm{C}^2$級関数$\bm{q}: \bm{r} \in \realNumbers^{3N} \mapsto \bm{q}(\bm{r}) \in \realNumbers^{3N}$として表せる状況を考える。
まず$\LC$は$t,\bm{q},\dot{\bm{q}}$の関数になる。なぜなら
\[ \dot{r_i} = \deriv{r_i(\bm{q})}{t}{} = \sum_{j=1}^N \partDeriv{r_i}{q_j}{}\dot{q_j} \]
となり、$\partDeriv{r_i}{q_j}{}$は$\bm{q}$の関数なので$\dot{\bm{r}}$が$\bm{q},\dot{\bm{q}}$の関数となるからである。全く同様にして$\dot{\bm{q}}$は$\bm{r},\dot{\bm{r}}$の関数となる。後々の計算の為に座標系$\bm{q}$上でのLagrange関数$L$を次式で定義しておく。
\[ L(t,\bm{q},\dot{\bm{q}}) \coloneqq \LC(t,\bm{r}(\bm{q}),\dot{\bm{r}}(\bm{q},\dot{\bm{q}})) \]
$L$と$\LC$は関数値は等しいが、写像としての定義が異なる。物理学ではそういうものを区別せずに、異なる座標系で同じ記号$L$を使いまわすのが慣例だが、ここでは式変形から手品を排除して全てをはっきりと見る為に敢えて執拗に数学の形式に拘ることにする。(「いやしかし、$\bm{r}$は既に$t$の関数として$\bm{r}(t)$と表しているのに、$\bm{q}$の関数として$\bm{r}(\bm{q})$として表すのはいい加減ではないか?」という指摘もあろう。その通りで、有言実行するには新たに記号を定義して区別するしかないが、それでは却って式の可読性が下がる。結局、厳密さによる混乱の回避の恩恵と式の可読性のトレードオフで戦略を決めている。)$L$を$\LC$で表したのと同じ理屈で次式も成り立つ。\[ \LC(t,\bm{r},\dot{\bm{r}}) = L(t,\bm{q}(\bm{r}),\dot{\bm{q}}(\bm{r},\dot{\bm{r}})) \]
座標変換によって$\nabla_\bm{r}\LC$がどうなるか考える。
\begin{align*} \partDerivLong{\LC(t,\bm{r},\dot{\bm{r}})}{r_i}{} &= \partDerivLong{L(t,\bm{q}(\bm{r}),\dot{\bm{q}}(\bm{r},\dot{\bm{r}}))}{r_i}{} \\ &= \sum_{j=1}^N \left(\partDerivLong{L(t,\bm{q},\dot{\bm{q}})}{q_j}{}\right)\partDeriv{q_j}{r_i}{} + \sum_{j=1}^N \left(\partDerivLong{L(t,\bm{q},\dot{\bm{q}})}{\dot{q_j}}{}\right)\partDeriv{\dot{q_j}}{r_i}{} \end{align*}ここで$N$次正方行列$A$を$A_{i,j} = \partDeriv{q_i}{r_j}{}$で定義すると、これは関数$\bm{r}$のJacobianであり、関数$\bm{r}$は可逆だから$A$は正則である。同様に$N$次正方行列$B$(正則とは限らない)を$B_{i,j} = \partDeriv{\dot{q_i}}{r_j}{}$で定義すると次式を得る。
\begin{equation} \label{LCのrによる微分をLのqによる微分で表す式} \nabla_\bm{r}\LC = A^\top\nabla_\bm{q}L + B^\top\nabla_{\dot{\bm{q}}}L \tag{2} \end{equation} 次に座標変換によって$\nabla_{\dot{\bm{r}}}\LC$がどうなるか考える。
\[ \partDerivLong{\LC}{\dot{r_i}}{}(t,\bm{r},\dot{\bm{r}}) = \partDerivLong{L(t,\bm{q}(\bm{r}),\dot{\bm{q}}(\bm{r},\dot{\bm{r}}))}{\dot{r_i}}{} \nonumber = \sum_{j=1}^N \left(\partDerivLong{L(t,\bm{q},\dot{\bm{q}})}{\dot{q_j}}{}\right)\partDeriv{\dot{q_j}}{\dot{r_i}}{} \]
ここで
\[ \dot{q_i} = \deriv{q_i(\bm{r})}{t}{} = \sum_{j=1}^N \partDeriv{q_i}{r_j}{}\dot{r_j} \]
より
\[ \partDeriv{\dot{q_i}}{\dot{r_j}}{} = \partDeriv{q_i}{r_j}{} = A_{i,j} \]
であるから次式を得る。
\[ \nabla_{\dot{\bm{r}}}\LC = A^\top \nabla_{\dot{\bm{q}}}L \]
これをさらに$t$で微分すると
次に座標変換によって$\nabla_\bm{r} \gCi$がどうなるか考える。$L$を定義したときと同じように、$g_i(\bm{q}) \coloneqq \gCi(\bm{r}(\bm{q}))$とすると$\gCi(\bm{r}) = g_i(\bm{q}(\bm{r}))$である。
\[ \partDerivLong{\gCi(\bm{r})}{r_i}{} = \partDerivLong{g(\bm{q}(\bm{r}))}{r_i}{} = \sum_{j=1}^N \partDerivLong{g(\bm{q})}{q_j}{}\partDeriv{q_j}{r_i}{} \]
よって次式が成り立つ。
以上の式\eqref{LCのrによる微分をLのqによる微分で表す式},\eqref{LCの速度による微分の時間微分をLの一般化速度による微分の時間微分で表す式},\eqref{gCのrによる微分をgのqによる微分で表す式}を\eqref{直角座標系に於けるNewtonの運動方程式}に適用すると次式を得る。
\[ A^\top\left(\nabla_\bm{q}L – \derivLong{\nabla_{\dot{\bm{q}}}L}{t}{} + \sum_{i=1}^{N_C} \lambda_i(t)\nabla_\bm{q} g_i\right) + \left(B^\top – \left(\derivLong{A^\top}{t}{}\right)\right)\nabla_{\dot{\bm{q}}}L = \bm{0} \]
$B^\top – \derivLong{A^\top}{t}{} = O$となることを示す。まず
\[ B_{i,j} = \partDeriv{\dot{q_i}}{r_j}{} = \partDerivLong{\deriv{q_i(\bm{r})}{t}{}}{r_j}{} = \partDerivLong{\sum_{k=1}^N \partDeriv{q_i}{r_k}{}\dot{r_k}}{r_j}{} = \sum_{k=1}^N \partDerivIIHetero{q_i}{r_j}{r_k}\dot{r_k} \]
次に
\[ \deriv{A_{i,j}}{t}{} = \derivLong{\partDeriv{q_i}{r_j}{}}{t}{} = \sum_{k=1}^N \partDerivIIHetero{q_i}{r_k}{r_j}\dot{r_k} = \sum_{k=1}^N \partDerivIIHetero{q_i}{r_j}{r_k}\dot{r_k} = B_{i,j} \]
である。左から2つ目の等号は、$\partDeriv{q_i}{r_j}{}$が$\bm{r}$の関数である($q_i$は$\bm{r}$の関数なのでそれを$r_j$で偏微分しても$\bm{r}$の関数である)ことから従う。右から2つ目の等号は$\bm{q}$が$\bm{r}$の$\mathrm{C}^2$級関数であと仮定しておいたことから従う。以上2つの式から$B^\top – \derivLong{A^\top}{t}{} = O$であるので結局次式を得る。
\[ A^\top\left(\nabla_\bm{q}L – \derivLong{\nabla_{\dot{\bm{q}}}L}{t}{} + \nabla_\bm{q} g_i\right) = \bm{0} \]
先述の通り$A$は正則なので両辺に左から${A^\top}^{-1}$を掛けて次式を得る
\[ \nabla_\bm{q}L – \derivLong{\nabla_{\dot{\bm{q}}}L}{t}{} + \sum_{i=1}^{N_C} \lambda_i(t)\nabla_\bm{q} g_i = \bm{0} \]
これと制約条件を合わせて、座標変換後の拘束条件付きのLagrangeの運動方程式は次式である。
Lagrange関数と拘束条件式の記号が変わった以外は直角座標系のときと同じ形の式である。
座標変換を工夫すると制約なしのLagrangeの運動方程式が得られる可能性について
式\eqref{一般化座標系に於けるLagrangeの運動方程式}は$3N$行の連立微分方程式であるが、$\bm{q}$の取り方を工夫することで$\nabla_\bm{q} g_k$の幾つかの行を0にできる。$q_1,\dotsc,q_{3N}$のうち$g_k(\bm{q})\;(k=1,\dotsc,\NC)$に現れるものの個数が最小になるような$\bm{q}$を見つけると都合が良い。もし$q_i$が$g_k(\bm{q})$に現れなければ$\nabla_\bm{q} g_k$の$i$行目は0である。そして$g_k(\bm{q}) = 0\;(k=1,\dotsc,\NC)$に現れる$\bm{q}$の成分が簡単に求まる場合、残った成分について拘束なしのLagrangeの運動方程式(Euler–Lagrange方程式とかLagrange’s equations of the second kind (第二種Lagrange方程式)と呼ばれる)を解けば良いので問題が格段に扱いやすくなる。
物理学を道具として用いる分野の技術書等(例えば制御工学)では普通、最初から拘束条件が消えるような一般化座標系への変換を考えてLagrange関数を構築して拘束なしのLagrangeの運動方程式を鮮やかに立てているが、これは「拘束条件が消えるような一般化座標系への変換を考え」る過程で自動的に「$g_k(\bm{q}) = 0\;(k=1,\dotsc,\NC)$に現れる$\bm{q}$の成分が簡単に求ま」って、そして「$q_i$が$g_k(\bm{q})$に現れなければ$\nabla_\bm{q} g_k$の$i$行目は0」となって、最初から拘束なしのLagrangeの運動方程式に辿り着ているのである。
問題例
$N=1, \NC=1$とし、質点の質量を$m$とする。拘束条件として潰れた楕円形の閉曲面$0 = g_\text{C}(\bm{r}): = {r_1}^2 + \frac{1}{4}{r_2}^2 + \frac{1}{9}{r_3}^2 – 1$を考える。$r_3$軸の負の向きに重力加速度$g$が働くとする。
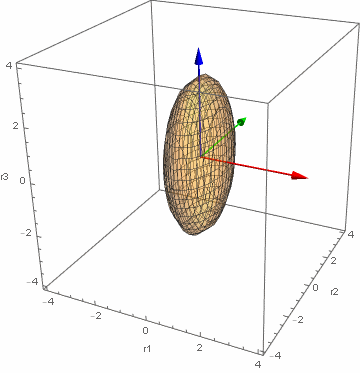
Lagrange関数は次式である。
$$ \LC(t,\bm{r},\dot{\bm{r}}) = \frac{1}{2}m\|\dot{\bm{r}}\|^2 – gr_3 $$直角座標系に於ける拘束条件付きのLagrangeの運動方程式を具体的に書き下すと次のようになる。
$$ \begin{cases} \begin{bmatrix} 0 \\ 0 \\ -g \end{bmatrix} – m \begin{bmatrix} \ddot{r_1} \\ \ddot{r_2} \\ \ddot{r_3} \end{bmatrix} + \lambda(t) \begin{bmatrix} 2r_1 \\ \frac{1}{2}r_2 \\ \frac{2}{9}r_3 \end{bmatrix} = \begin{bmatrix} 0 \\ 0 \\ 0 \end{bmatrix} \\ {r_1}^2 + \frac{1}{4}{r_2}^2 + \frac{1}{9}{r_3}^2 = 1 \end{cases} $$人間に解けるような問題ではないから計算機で数値計算するとして、拘束条件が厄介である。そこで次のような座標変換を考える。
$$ \begin{cases} r_1 &= q_3 \sin q_1 \cos q_2 \\ r_2 &= 2q_3\sin q_1 \sin q_2 \\ r_3 &= 3q_3\cos q_1 \\ q_3 &\geq 0 \end{cases} $$そうすると拘束条件は
$$ 0 = g(\bm{q}) = g_\text{C}(\bm{r}(\bm{q})) = {q_3}^2 – 1 $$となり$q_3 = 1$が決まる。そして$\nabla_\bm{q}g$は次式になる。
$$ \nabla_\bm{q}g(\bm{q}) = \begin{bmatrix} 0 \\ 0 \\ 2q_3 \end{bmatrix} $$そしてLagrange関数を$t,\bm{q},\dot{\bm{q}}$の関数で表して$\bm{q},\dot{\bm{q}}$で偏微分してLagrangeの運動方程式を立てるのだが、実はここから先の計算は恐ろしく大変である。筆者の手作業では1日掛かっても終わりそうにないのでMathematicaにやらせたが、Lagrangeの運動方程式に至ってはここに書けないほど長い数式になった。簡単に表せる部分のみ具体的に表示し、他は記号的に書くと次のようになる。
$$ \begin{align} \begin{bmatrix} \partDerivLong{L(t,\bm{q},\dot{\bm{q}})}{q_1}{} \\ \partDerivLong{L(t,\bm{q},\dot{\bm{q}})}{q_2}{} \\ \partDerivLong{L(t,\bm{q},\dot{\bm{q}})}{q_3}{} \end{bmatrix} – \derivLong{ \begin{bmatrix} \partDerivLong{L(t,\bm{q},\dot{\bm{q}})}{\dot{q_1}}{} \\ \partDerivLong{L(t,\bm{q},\dot{\bm{q}})}{\dot{q_2}}{} \\ \partDerivLong{L(t,\bm{q},\dot{\bm{q}})}{\dot{q_3}}{} \end{bmatrix} }{t}{} + \lambda(t) \begin{bmatrix} 0 \\ 0 \\ 2q_3 \end{bmatrix} &= \begin{bmatrix} 0 \\ 0 \\ 0 \end{bmatrix} \label{問題例の一般化座標系に於けるLagrangeの運動方程式} \\ q_3 &= 1 \end{align} $$式\eqref{問題例の一般化座標系に於けるLagrangeの運動方程式}の3行目は$L(t,\bm{q},\dot{\bm{q}})$に$q_3=1$を代入する前に計算しなければならないことに注意する(1,2行目は$q_3=1$を先に代入してから計算しても構わない)。そもそも式\eqref{問題例の一般化座標系に於けるLagrangeの運動方程式}は$q_3$が変数であるとして導出されたのだから、\eqref{問題例の一般化座標系に於けるLagrangeの運動方程式}の計算前に$q_3$を特定の値で固定してはいけない。例えば$f: x\mapsto x^2$という写像があって、何らかの条件から$x(t)\equiv 1$であることが解っているからといって$\partDerivLong{f(x(t))}{x(t)}{} = 0$とするのはおかしい。$\partDerivLong{f(x(t))}{x(t)}{} = 2x(t)$なので$x(t)\equiv 1$であっても$\partDerivLong{f(x(t))}{x(t)}{} = 2 \neq 0$である。「関数の定義」と「関数値」は別物であって、「関数の定義」は「関数値」よりも多くの情報を保持している。偏微分は「関数の値」ではなく「関数の定義」に対して定められている。
式\eqref{問題例の一般化座標系に於けるLagrangeの運動方程式}の上2行は$\nabla_\bm{q}g$の要素が0になっており、$\lambda(t)$の影響を受けない。既に$q_3(t)=1$は解っていて未知の座標変数は$q_1(t),q_2(t)$の2つだけであるから式\eqref{問題例の一般化座標系に於けるLagrangeの運動方程式}の上2行からこれらが唯一に決定されるように思えるし、そうであって欲しい。そして実際にそうでなくてはならない。仮に式\eqref{問題例の一般化座標系に於けるLagrangeの運動方程式}の上2行だけで$q_1(t),q_2(t)$が唯一に決定されないとする。これ以外に利用できる情報は3行目の式しか残されていなが、それを考慮に入れたところで、$\lambda(t)$が同時に解くべき未知変数に追加されるため、結局解けないのである。古典力学的に正しく定義された問題に対しては解が唯一に決まることは疑いようのない事実であり、「$q_1(t),q_2(t)$が唯一に決まらない」状況は物理的に許されず、式\eqref{問題例の一般化座標系に於けるLagrangeの運動方程式}の上2行だけで$q_1(t),q_2(t)$が唯一に決定されるより他にあり得ないのである。そして3行目から$\lambda(t)$が決定される。
先にも述べた、解析力学の理解を前提とした技術書では座標変換で一般化座標変数の一部を制約条件から事前に求めてしまい(制約条件と同じ個数の座標変数が代数的に決まることを想定する)、それらを最初から定数とした上で、Lagrange関数を残りの一般化座標の関数と見做して拘束なしの運動方程式を解いている。こうして$\lambda(t)$を表に出さずに解軌道に辿り着く。
この一般化座標系に於けるLagrangeの運動方程式をMathematicaで解いた結果を元の座標系に変換して可視化したものが次の図である。
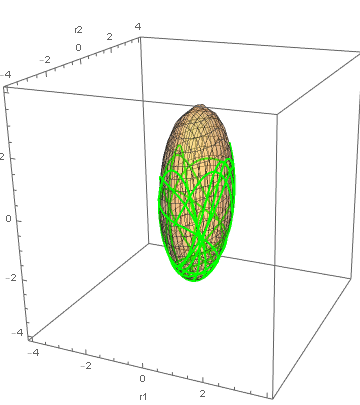
初期条件は$q_1(0) = \pi/3, q_2(0) = \pi/4, \dot{q_1}(0) = \dot{q_2}(0) = 0$すなわち$\bm{r}(0) = [\sqrt{6}/4,\sqrt{6}/2,3/2]^\top,\;\dot{\bm{r}}(0)=\bm{0}$である。この位置に固定されていた質点が時刻0に解放されて楕円曲面に拘束されながら重力によって落下し、底に辿り着くと勢いで壁を登っていき、速度が落ちて再び落下していくのを繰り返す様子が見える。
以下は、このシミュレーションを行ったMathematicaノートブックである。