はじめに
パラボラ・アンテナに関して次の 2 つの性質を証明する。
- 軸に平行に入射した光線が焦点を通ること
- 軸に垂直な平面 S から発して軸に平行に入射した光線が焦点 F に至るまでの距離が S 上の位置に依らないこと
⇒入射する平面波は焦点に同位相で集まる
\[
% general purpose
\newcommand{\ctext}[1]{\raise0.2ex\hbox{\textcircled{\scriptsize{#1}}}}
% mathematics
% general purpose
\DeclarePairedDelimiterX{\parens}[1]{\lparen}{\rparen}{#1}
\DeclarePairedDelimiterX{\braces}[1]{\lbrace}{\rbrace}{#1}
\DeclarePairedDelimiterX{\bracks}[1]{\lbrack}{\rbrack}{#1}
\DeclarePairedDelimiterX{\verts}[1]{|}{|}{#1}
\DeclarePairedDelimiterX{\Verts}[1]{\|}{\|}{#1}
\newcommand{\as}{{\quad\textrm{as}\quad}}
\newcommand{\st}{{\textrm{ s.t. }}}
\DeclarePairedDelimiterX{\setComprehension}[2]{\lbrace}{\rbrace}{#1\,\delimsize\vert\,#2}
\newcommand{\naturalNumbers}{\mathbb{N}}
\newcommand{\integers}{\mathbb{Z}}
\newcommand{\rationalNumbers}{\mathbb{Q}}
\newcommand{\realNumbers}{\mathbb{R}}
\newcommand{\complexNumbers}{\mathbb{C}}
\newcommand{\field}{\mathbb{F}}
\newcommand{\func}[2]{{#1}\parens*{#2}}
\newcommand*{\argmax}{\operatorname*{arg~max}}
\newcommand*{\argmin}{\operatorname*{arg~min}}
% set theory
\newcommand{\range}[2]{\braces*{#1,\dotsc,#2}}
\providecommand{\complement}{}\renewcommand{\complement}{\mathrm{c}}
\newcommand{\ind}[2]{\mathbbm{1}_{#1}\parens*{#2}}
\newcommand{\indII}[1]{\mathbbm{1}\braces*{#1}}
% number theory
\newcommand{\abs}[1]{\verts*{#1}}
\newcommand{\combi}[2]{{_{#1}\mathrm{C}_{#2}}}
\newcommand{\perm}[2]{{_{#1}\mathrm{P}_{#2}}}
\newcommand{\GaloisField}[1]{\mathrm{GF}\parens*{#1}}
% analysis
\newcommand{\NapierE}{\mathrm{e}}
\newcommand{\sgn}[1]{\operatorname{sgn}\parens*{#1}}
\newcommand*{\rect}{\operatorname{rect}}
\newcommand{\cl}[1]{\operatorname{cl}#1}
\newcommand{\Img}[1]{\operatorname{Img}\parens*{#1}}
\newcommand{\dom}[1]{\operatorname{dom}\parens*{#1}}
\newcommand{\norm}[1]{\Verts*{#1}}
\newcommand{\floor}[1]{\left\lfloor#1\right\rfloor}
\newcommand{\ceil}[1]{\left\lceil#1\right\rceil}
\newcommand{\expo}[1]{\exp\parens*{#1}}
\newcommand{\sinc}{\operatorname{sinc}}
\newcommand{\nsinc}{\operatorname{nsinc}}
\newcommand{\GammaFunc}[1]{\Gamma\parens*{#1}}
\newcommand*{\erf}{\operatorname{erf}}
% inverse trigonometric functions
\newcommand{\asin}[1]{\operatorname{Sin}^{-1}{#1}}
\newcommand{\acos}[1]{\operatorname{Cos}^{-1}{#1}}
\newcommand{\atan}[1]{\operatorname{{Tan}^{-1}}{#1}}
\newcommand{\atanEx}[2]{\atan{\parens*{#1,#2}}}
% convolution
\newcommand{\cycConv}[2]{{#1}\underset{\text{cyc}}{*}{#2}}
% derivative
\newcommand{\deriv}[3]{\frac{\operatorname{d}^{#3}#1}{\operatorname{d}{#2}^{#3}}}
\newcommand{\derivLong}[3]{\frac{\operatorname{d}^{#3}}{\operatorname{d}{#2}^{#3}}#1}
\newcommand{\partDeriv}[3]{\frac{\operatorname{\partial}^{#3}#1}{\operatorname{\partial}{#2}^{#3}}}
\newcommand{\partDerivLong}[3]{\frac{\operatorname{\partial}^{#3}}{\operatorname{\partial}{#2}^{#3}}#1}
\newcommand{\partDerivIIHetero}[3]{\frac{\operatorname{\partial}^2#1}{\partial#2\operatorname{\partial}#3}}
\newcommand{\partDerivIIHeteroLong}[3]{{\frac{\operatorname{\partial}^2}{\partial#2\operatorname{\partial}#3}#1}}
% integral
\newcommand{\integrate}[5]{\int_{#1}^{#2}{#3}{\mathrm{d}^{#4}}#5}
\newcommand{\LebInteg}[4]{\int_{#1} {#2} {#3}\parens*{\mathrm{d}#4}}
% complex analysis
\newcommand{\conj}[1]{\overline{#1}}
\providecommand{\Re}{}\renewcommand{\Re}[1]{{\operatorname{Re}{\parens*{#1}}}}
\providecommand{\Im}{}\renewcommand{\Im}[1]{{\operatorname{Im}{\parens*{#1}}}}
\newcommand*{\Arg}{\operatorname{Arg}}
\newcommand*{\Log}{\operatorname{Log}}
% Laplace transform
\newcommand{\LPLC}[1]{\operatorname{\mathcal{L}}\parens*{#1}}
\newcommand{\ILPLC}[1]{\operatorname{\mathcal{L}}^{-1}\parens*{#1}}
% Discrete Fourier Transform
\newcommand{\DFT}[1]{\mathrm{DFT}\parens*{#1}}
% Z transform
\newcommand{\ZTrans}[1]{\operatorname{\mathcal{Z}}\parens*{#1}}
\newcommand{\IZTrans}[1]{\operatorname{\mathcal{Z}}^{-1}\parens*{#1}}
% linear algebra
\newcommand{\bm}[1]{{\boldsymbol{#1}}}
\newcommand{\matEntry}[3]{#1\bracks*{#2}\bracks*{#3}}
\newcommand{\matPart}[5]{\matEntry{#1}{#2:#3}{#4:#5}}
\newcommand{\diag}[1]{\operatorname{diag}\parens*{#1}}
\newcommand{\tr}[1]{\operatorname{tr}{\parens*{#1}}}
\newcommand{\inprod}[2]{\left\langle#1,#2\right\rangle}
\newcommand{\HadamardProd}{\odot}
\newcommand{\HadamardDiv}{\oslash}
\newcommand{\Span}[1]{\operatorname{span}\bracks*{#1}}
\newcommand{\Ker}[1]{\operatorname{Ker}\parens*{#1}}
\newcommand{\rank}[1]{\operatorname{rank}\parens*{#1}}
% vector
% unit vector
\newcommand{\vix}{\bm{i}_x}
\newcommand{\viy}{\bm{i}_y}
\newcommand{\viz}{\bm{i}_z}
% probability theory
\newcommand{\PDF}[2]{\operatorname{PDF}\bracks*{#1,\;#2}}
\newcommand{\Ber}[1]{\operatorname{Ber}\parens*{#1}}
\newcommand{\Beta}[2]{\operatorname{Beta}\parens*{#1,#2}}
\newcommand{\ExpDist}[1]{\operatorname{ExpDist}\parens*{#1}}
\newcommand{\ErlangDist}[2]{\operatorname{ErlangDist}\parens*{#1,#2}}
\newcommand{\PoissonDist}[1]{\operatorname{PoissonDist}\parens*{#1}}
\newcommand{\GammaDist}[2]{\operatorname{Gamma}\parens*{#1,#2}}
\newcommand{\cind}[2]{\ind{#1\left| #2\right.}} % conditional indicator function
\providecommand{\Pr}{}\renewcommand{\Pr}[1]{\operatorname{Pr}\parens*{#1}}
\DeclarePairedDelimiterX{\cPrParens}[2]{(}{)}{#1\,\delimsize\vert\,#2}
\newcommand{\cPr}[2]{\operatorname{Pr}\cPrParens{#1}{#2}}
\newcommand{\E}[2]{\operatorname{E}_{#1}\bracks*{#2}}
\newcommand{\cE}[3]{\E{#1}{\left.#2\right|#3}}
\newcommand{\Var}[2]{\operatorname{Var}_{#1}\bracks*{#2}}
\newcommand{\Cov}[2]{\operatorname{Cov}\bracks*{#1,#2}}
\newcommand{\CovMat}[1]{\operatorname{Cov}\bracks*{#1}}
% graph theory
\newcommand{\neighborhood}{\mathcal{N}}
% programming
\newcommand{\plpl}{\mathrel{++}}
\newcommand{\pleq}{\mathrel{+}=}
\newcommand{\asteq}{\mathrel{*}=}
\]
\[
\newcommand{\xIcdt}{x_\text{i}}
\newcommand{\xIcdtZero}{x_{\text{i},0}}
\newcommand{\xIcdtOne}{x_{\text{i},1}}
\newcommand{\frZero}{f_{\text{r},0}}
\newcommand{\frOne}{f_{\text{r},1}}
\]
軸に平行に入射した光線が焦点を通ること
回転放物面を軸に平行な平面で切った断面について考えればよい。断面の方程式が $f(x) = ax^2$ であるとする。放物線の点 $P(\xIcdt, f(\xIcdt))$ （i は incident の意味）に向かって軸に平行に入射する光線を考える。$\xIcdt=0$ のときは来た道を戻ることは明らかである。以降では $\xIcdt\neq 0$ とする。
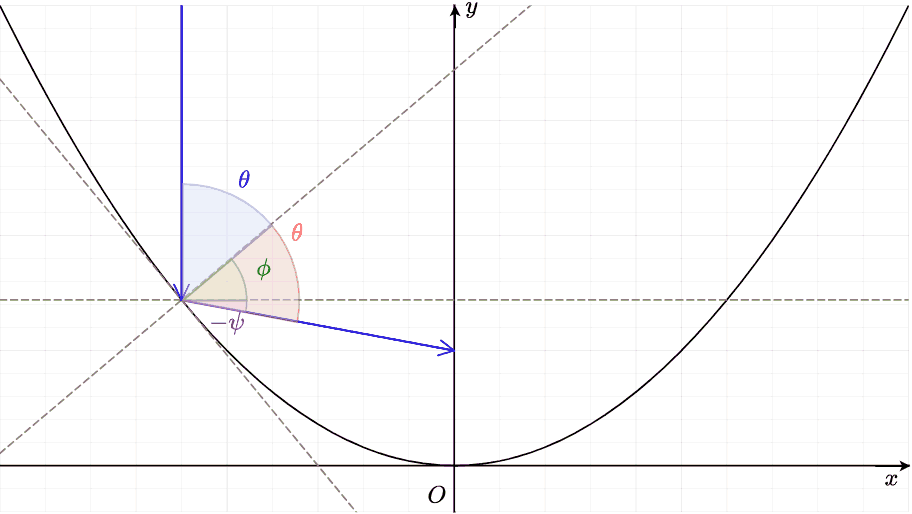光軸に平行に入射した光線が焦点に至るまでの軌跡
点 $P$ に於ける放物線の内向きの法線ベクトルが $x$ 軸と成す角度を $\phi$ とする。光線の入射角はこの法線ベクトルから、入射する光線に向かって測った角度であり、これを $\theta$ とする。反射する光線が $x$ 軸と成す角度を $\psi$ とする。
点 $2a\xIcdt$ に於ける接線の傾きは $2a\xIcdt$ であり、法線の傾きは $\tan\phi = -1/(2a\xIcdt)$ である。入射角について次式が成り立つ。
\[\tan\theta = \tan\parens{\pi/2 – \phi} = \frac{1}{\tan\phi} = -2a\xIcdt\]
反射する光線に対応する直線の傾きについて次式が成り立つ。
\[\tan\psi = \tan\parens{\pi/2 – 2\theta} = \frac{1}{\tan2\theta} = \frac{1 – \tan^2\theta}{2\tan\theta} = \frac{4 a^2 \xIcdt^2 – 1}{4a\xIcdt}\]
反射する光線に対応する直線 $y=f_\text{r}(x) は次式である。
\[f_\text{r}(x) = (\tan\psi)(x-\xIcdt) + f(\xIcdt) = a\xIcdt^2 – \frac{4 a^2 \xIcdt^2 – 1}{4a\xIcdt}(x-\xIcdt)\]
$\xIcdt$ として互いに異なる非零の二つの値 $\xIcdtZero$ と $\xIcdtOne$ を考える。それぞれについて反射する光線に対応する直線 $y=\frZero(x),\;y=\frOne(x)$ は次式である。
\[
\begin{align*}
\frZero(x) &= a\xIcdtZero^2 – \frac{4 a^2 \xIcdtZero^2 – 1}{4a\xIcdtZero}(x-\xIcdtZero) \\
\frOne(x) &= a\xIcdtOne^2 – \frac{4 a^2 \xIcdtOne^2 – 1}{4a\xIcdtOne}(x-\xIcdtOne)
\end{align*}
\]
この 2 つの直線の交点を計算すると $(0,1/4a)$ である（計算は難しくない）。つまり光線が放物線上のどこに入射しようと、必ずこの点を通る。これが焦点である。
軸に垂直な平面 S から発して軸に平行に入射した光線が焦点 F に至るまでの距離が S 上の位置に依らないこと
\[
\newcommand{\xMax}{x_\text{max}}
\]
軸に平行に入射する 2 本の光線を考え、$x$ 座標をそれぞれ $\xIcdtZero,\;\xIcdtOne$ とする。但し $\abs{\xIcdtZero},\;\abs{\xIcdtOne} \leq \xMax\;(\xMax>0)$ である。この光線が $y$ 軸の正の向きの遠方から飛来して直線 $y=a\xMax^2$ に達した位置から焦点 $F$ に至るまでの距離（次の図中の青色と緑色の各経路の長さ）が等しいことを示す。
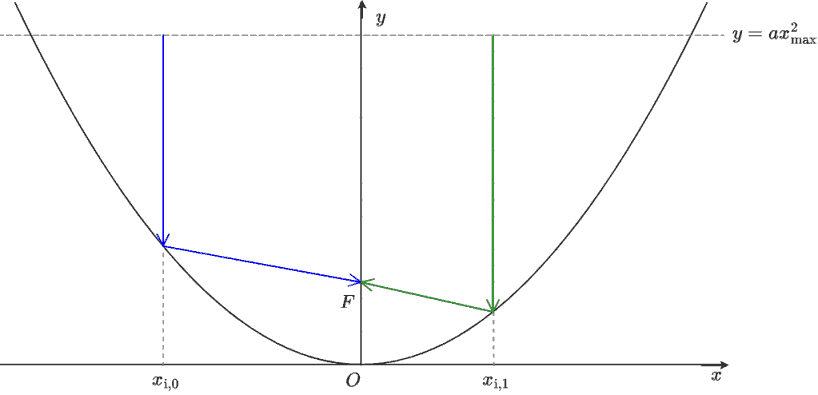光軸に平行に入射した 2 本の光線が焦点に至るまでの軌跡
青く示した経路の長さ $l_0$ は次式である。
\[ l_0 = a\xMax^2 – a\xIcdtZero^2 + \sqrt{\xIcdtZero^2 + (a\xIcdtZero^2 – 1/(4a))^2} \]
根号の中身を評価する。
\begin{align*}
\xIcdtZero^2 + (a\xIcdtZero^2 – 1/(4a))^2 &= \xIcdtZero^2 + a^2\parens*{\xIcdtZero^2 – \frac{1}{(2a)^2}}^2 = \xIcdtZero^2 + a^2\parens*{\xIcdtZero^4 + \frac{1}{(2a)^4} – \frac{2\xIcdtZero^2}{(2a)^2}} \\
&= a^2\xIcdtZero^4 + \frac{\xIcdtZero^2}{2} + \frac{a^2}{(2a)^4} = \parens*{a\xIcdtZero^2 + \frac{a}{(2a)^2}}^2 = \parens*{a\xIcdtZero^2 + \frac{1}{4a}}^2
\end{align*}
よって次式が成り立つ。
\[ l_0 = a\xMax^2 + 1/(4a) \]
$l_0$ が $\xIcdtZero$ に依存していない。全く同様にして $l_1 = a\xMax^2 + 1/(4a)$ が示され、 2 つの経路の長さが等しいことが解る。
投稿者: motchy
An embedded software and FPGA engineer for measuring instrument.
motchy のすべての投稿を表示
