線状電荷が作る電界

はじめに

平行 2 線式線路や同軸ケーブルの特性インピーダンスの公式を導出する過程で、直線状に分布した電荷が線路の微小な長さの区間に作る電界を求めることになる。その際、線路が十分に長いので、電界のうち線路に平行な成分は垂直な成分に比べて十分に小さく無視できると仮定する。本記事ではこの近似がどの程度信頼できるのかを、計算してイメージを掴んでみる。

状況

次の図のように x 軸上に線状電荷が Q [C/m] (Q>0) で分布している。ただし x 軸の負と正の両側で分布している長さは異なる。

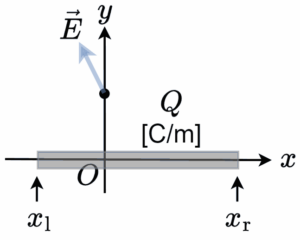
このときに点 (0,d) の電界は次式である（Gauss の法則から導かれる）。

$$\mathit{E}={\mathit{i}}_x\frac{1}{2\pi \epsilon }{\int }_{x_l}^{x_r}\frac{-x}{(x^2+d^2{)}^{3/2}}{\mathrm{d}}^{}x+{\mathit{i}}_y\frac{1}{2\pi \epsilon }{\int }_{x_l}^{x_r}\frac{d}{(x^2+d^2{)}^{3/2}}{\mathrm{d}}^{}x$$

ここに ${\mathit{i}}_x,{\mathit{i}}_y$ はそれぞれ x, y 軸方向の単位ベクトルであり、$\epsilon$ は空間の誘電率である。

計算

次の Mathematica ノートブックでは、前記の点 (0,d) に於ける電界を求め、y 成分に対して x 成分が無視できるほどに小さいことを確かめる。また $x_l=-x_r$ の場合の原点周辺に於ける電界を可視化する。